Today was the first time in a week that I found (or took?) some time to actually continue with Release. As said before – the next step I was going to do was to add “collision detection” between the approaching objects and the expanding shield.
There were – as usual – some things to consider. Not the least of them, I wanted the collision detection to be quite “exact” and I also wanted it to not take to much time – since there still are many things to add.
In the following I’ll describe the route taken.
First I added one precondition to my objects, all vectorlists (of objects) from now on (until changed 🙂 ) will start in the center of the object. That will probably make it necessary to have “mode” vectorlists. Here the current X enemy:

This is done, so that I only have to check the center for collision (plus possible offsets to accomodate the size of the object).
I thought quite a while about how to implement the detection, following thoughts (amongst others):
a) I know all the neighboring points of the (shield-) polygon, so I can check whether the point (center of object) is inside the polygon. The polygon could be devided into rectangles so I only check if one rectangle encloses the point. After checking available algorythms on the net – I thought about “dividing” the shield into triangles and check these.
-> But still the math to do exact checking would have been quite an undertaking in assembler and surely not be very efficient.
b) The corner points of the shield (the polygon) all lie on a circle around the center. So I can take the outer enclosing circle of the shield and check if the coordinate of the object is “smaller” if true – check also whether the objects coordinates are all greater than the inner exclosing circle, if so the object lies on the shield. (keeping in mind the cartesian coordinates of vectrex)
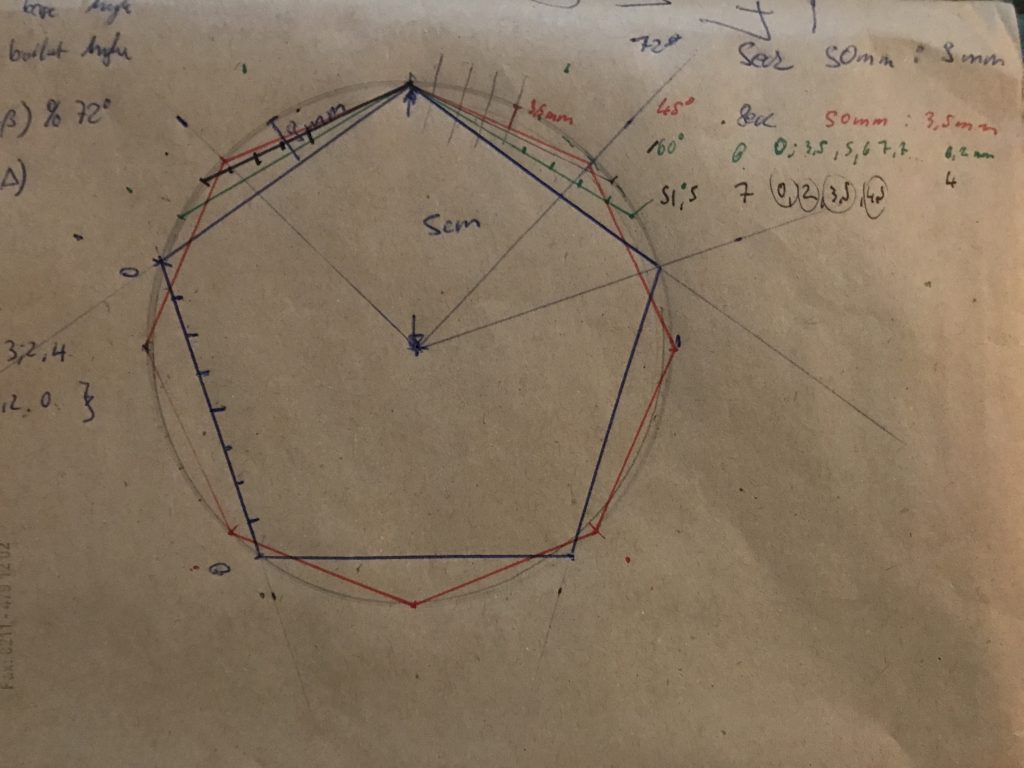
-> I implemented that, but it was a wield juggling of coordinates and the result was not as good as expected since (especially with the 5 sided shield) the circle is quite a way away from the “half line points” of the polygon (see image below).
After that I was forced to leave my computer behind and drive 30 km in my car. The complete 30 km was one entire traffic jam and it took more than two hours – BUT – my brain was free to go drifting and pondering the above. I think I came up with a very easy and FAST (cycles…) solution.
But one step after another… after reaching home I made following drawing to complete my thinking:
All (current) objects are positioned around the middle point (the base). The placement of the objects (including the shield) is done in relation to the center. All placings are done using only ONE move. So all coordinates share the same basis. Keeping this in mind in addition to variant b) from above – meaning that the shield can be seen as a degenerated circle – I do not have to check any coordinates at all!
I only have to check if the radiuses of the objects are the same (or overlap). That is very easy to do! The other thing about the “exactness” of the checking…
The radius of the enclosing circle of the polygon (see above) only matches the coordinates (5 sided polygon) in the five corners, all other points on one line are (partly) considerably smaller. All polygons used for the base are regular:
- 5 sided – dividing the circle into 5 equal parts, every 72 degrees
- 6 sided – dividing the circle into 6 equal parts, every 60 degrees
- 7 sided – dividing the circle into 7 equal parts, every 52 degrees (aproximately)
- 8 sided – dividing the circle into 8 equal parts, every 45 degrees
This also means, that every x (72, 60, 52 and 45) degrees the differences between the polygon and the circle coordinate repeat (I chose to ignore the inner mirroring for now – I do not habe to save memory yet).
Since I did not want to do the math (and I don’t think math needs to be correct here, the vectrex doesn’t do floating points anyway) – I drew above picture and actually MEASURED the distances – you can see the divisions of the different polygon lines – and wrote them down to scale.
My first thought was to divide one side in ten equal parts, measure the distance and implement a look uptable. But doing more thinking and realizing that I would need a division to (yeah, if I divide something I need a division – brilliant thinking) – I skipped the division part and implemented a lookup table for each above repitious angles.
So the actual collision detection now goes like this:
a) check if the shields enclosing (outer) and exclosing (inner) circle are greater or lower (respectivly) if yes, than no collision, otherwise do
b) build the difference of the shield angle (since it is constantly moving/circling) and the angle of the object (yes – thankfully every object is instantiated with an angle to the center). The resulting difference is the angle we must inspect (see image 12, o’clock would be 0 degrees)
c) the resulting angles modulo in respect to the side count is build (72, 60, 52 or 45)
d) that modulo can be directly taken as an offset to the actual “polygon_correction_table” of the used polygon
e) the scale factor of the inner and outer shield wall is taken, updated with above build correction and compared to the scale factor of the object
done!
For completeness sake – here a copy of the source for those interested:
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ; u pointer to object being tested ; relevant data in u, SCALE ; routine tests if object hits the shield ; return a = 0 -> no ; return a = 1 -> yes ; u is preserved ; expects polygon correction table of the current shield polygon set to X ; ; trying to figure out whether the current object ; mathematically lies on the area of the shield is ; quite bothersome - so I take a shortcut here ; since I know the current angle of the base and the "angle" of the object ; I can calculate the difference in angle ; both objects are drawn with the same scale ; knowing that the scale is actual the radius of a circle they are drawn ; around the middle point, I only have to check whether ; the object lies within the inner radius (scale) and the outer radius ; (scale) of the shield ; using a perfect circle while drawing a 5 sided polygon is ; error prone, but since I know the angle between the objects ; I can do some error correction to "circle" coordinates ; to simulate a n sided polygon ; for each sided x sided polygon slightly different error corrections ; are used ; using the radius and a polygon correction I ONLY ; have to check the scale value not even a single coordinate! ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ; ; n correction values correctionList: polygon_5_correction: ; 72 values db 0, 1, 2, 3, 4, 5, 6, 8, 10, 11 db 12, 13, 14, 15, 15, 16, 16, 16, 16, 17 db 17, 17, 17, 17, 17, 18, 18, 18, 18, 18 db 18, 18, 19, 19, 19, 19, 19, 19, 19, 19 db 19, 18, 18, 18, 18, 18, 18, 18, 17, 17 db 17, 17, 17, 17, 16, 16, 16, 16, 15, 15 db 14, 13, 12, 11, 10, 8, 6, 5, 3, 2 db 1, 0 polygon_6_correction: ; 60 values db 0, 1, 2, 3, 4, 6, 7, 8, 9, 10 db 10, 11, 11, 12, 12, 13, 13, 13, 13, 13 db 13, 13, 14, 14, 14, 14, 14, 14, 14, 14 db 14, 14, 14, 14, 14, 14, 14, 14, 13, 13 db 13, 13, 13, 13, 13, 12, 12, 11, 11, 10 db 10, 9, 8, 7, 6, 4, 3, 2, 1, 0 polygon_7_correction: ; 52 values db 0, 1, 1, 2, 3, 4, 5, 5, 6, 6 db 7, 7, 7, 8, 8, 8, 8, 8, 9, 9 db 9, 9, 9, 9, 8, 8, 8, 8, 8, 7 db 7, 7, 6, 6, 5, 5, 4, 3, 2, 1 db 1, 0 polygon_8_correction: ; 45 values db 0, 1, 1, 2, 3, 4, 5, 5, 6, 6 db 6, 7, 7, 7, 7, 7, 8, 8, 8, 8 db 8, 8, 8, 8, 8, 8, 8, 8, 8, 7 db 7, 7, 7, 7, 6, 6, 6, 5, 5, 4 db 3, 2, 1, 1, 0 maxOffsetValues: db 20,15,10,9 SHIELD_VARIANCE equ 5 out_notTouched clra rts onShield: ; first look if current object and shield are completely out of bounds lda shieldStart ; outer shield border cmpa #$ff bhs noadd_os1 adda #SHIELD_VARIANCE ; a little bit wider noadd_os1: cmpa SCALE,u ; compare outer border with object position bls out_notTouched ; branch if a (shield outer wall) is lower or same than pos (scale) of object suba shieldWidth suba #(2*SHIELD_VARIANCE) ; wider (to compensate size of object and irregulatity to circle coords) suba currentMaxOffset cmpa SCALE,u ; compare outer border with object position bhs out_notTouched ; branch if a (shield inner wall) is higher or same than pos (scale) of object ; now a more thorough check is needed ; if the shield were a perfect circle the above should be enough ldd ANGLE,u ; angle of object subd base_angle ; angle diff = object angle - base angle bpl isPositive_os addd #720 isPositive_os: MY_LSR_D ; half it (value now 0 - 360 ) tfr d,y GET_POLY_DIV ; load polygone "divider" to d (72, 60, 52 or 45) lsrb negb ; the following does a ; angle % poly divider ; (gets the angle modulo the polygon angle) getMod_os: leay b,y cmpy #0 ; lea does not influence carry :-( bpl getMod_os negb leay b,y ; mod done tfr y,d leay d,x ; now in y ; is the pointer to the correction table, for circle position correction of ; our object in relation to the shield polygon ; do the above check AGAIN now with correction values present lda shieldStart ; outer shield border cmpa #$ff bhs noadd_os2 adda #SHIELD_VARIANCE ; a little bit wider noadd_os2: suba ,y cmpa SCALE,u ; compare outer border with object position bls out_notTouched ; branch if a (shield outer wall) is lower or same than pos (scale) of object suba shieldWidth suba #(2*SHIELD_VARIANCE) ; wider cmpa SCALE,u ; compare outer border with object position bhs out_notTouched ; branch if a (shield inner wall) is higher or same than pos (scale) of object lda #1 rts
It works quite well – see video below: