Current affairs:
Since yesterday I try to think differently in regards how the shield might be implemented. Befor I thought doing a (fixed) vectorlist and drawing it on screen was the way.
Using scale factor for sizing and possibly some sort of rotation routine to calculate variations. The area would be filled with some kind of grid.
This sounds like it would use much computational ressources (rotation, grid, large vectorlists etc).
Yesterday I began trying different things out – the current “version” in my minds vectrex goes like this:
- have a list of circle coordinates (the base and the shield is always centered, so this should work out)
- the list will be quite large, I think about coordinates for 360° step-circle
- enhance vide (vedi) to create datalists of such coordinates: (oops, seems I already did this!)
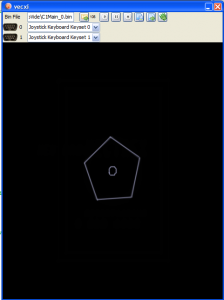
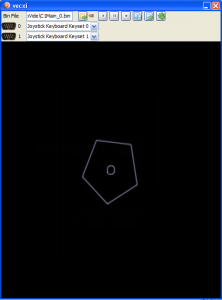
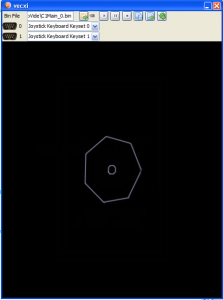
- with these circle coordinates I can easily calculate rotated or non rotated polygones
The algorythm goes like this:
e.g. for a 5-8 sided polygon:
(Note: for all code I’ll post, these are working and “thinking” version, and unless otherwise noted NOT optimized in any way!)
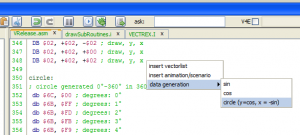
; builds to rotList ; in "angle" the angle to "rotate" (from 0 to 720 = 2 *360) since it is a 16 bit pointer angle! ; in "sided" the number of sides of the figure (regular figure, can be build by regular offsets in circle list) ; move coordinate is angle in circle list ; second and each following coordinate (n sided "add" in circle list) ; Ydrawvector = y2-y1 ; Xdrawvector = x2-x1 ; list generated will be format: ; db count ; db move y,x ; db draw y,x ; ... ; db draw y,x ; times two, since angle is a "list" of 16 bit values FIVE_ADD = (360/5)*2 SIX_ADD = (360/6)*2 SEVEN_ADD = (360/7)*2 EIGHT_ADD = (360/8)*2 ; buildRotatedNSidedFigure ldu #rotList lda sided deca sta tmp_count sta ,u+ ; count ; seek sidedness cmpa #4 bne test_n6 ldd #FIVE_ADD bra brnsf1 test_n6: cmpa #5 bne test_n7 ldd #SIX_ADD bra brnsf1 test_n7: cmpa #6 bne test_n8 ldd #SEVEN_ADD bra brnsf1 test_n8: ldd #EIGHT_ADD brnsf1: std tmp_add ; add to angle for n sided polygon ldd angle std tmp_angle ldx #circle ldd d,x std ,u++ ; move std tmp_lastpos ; now the sided next_brnsf: ldd tmp_angle addd tmp_add cmpd #(360*2) blo brnsf2 subd #(360*2) brnsf2 std tmp_angle ldd d,x ; a = y2, b = x2 tfr d,y ; now we must build the y2-y1 etc part suba tmp_lastpos ; y2-y1 sta ,u+ ; store y move subb tmp_lastpos+1 ; x2-x1 stb ,u+ ; store x move sty tmp_lastpos dec tmp_count bpl next_brnsf rts
With that routine I can build vectorlists of 5-8 sided regular polygons at any angle around a center. Without a MUL or otherwise difficult and time consuming calculation:
I plan to implement the shield also differently:
- have one inner and outer “ring”
- in between draw only a couple of “rings” (depending on the width of the shield) that oscillate from the inner to the outer “ring” and thus display the danger area
That I have yet to try out.
Next steps (probably):
- do the above shield
- do a starfield simulation
- add a first enemy
- add score
BTW.
It seems I have attracted a chiptune artist that might build a nice tune for this game – hip hip hurray!